↓Skip to main content
A cup of beer
  1. Posts/

做个编译器——词法分析实现

·374 words·2 mins
笔记
Table of Contents

General #

目的 #

The goal is to partition the string. This is implemented by reading left-to-right.（把字符串做拆分，并且是左到右的扫描。）

“Lookahead” may be required to decide where one token ends and the next token begins.（可能需要提前读入，来判断lexeme的边界）

Identify the token of each lexeme（把各lexemes识别成token）

实现词法分析的思路 #

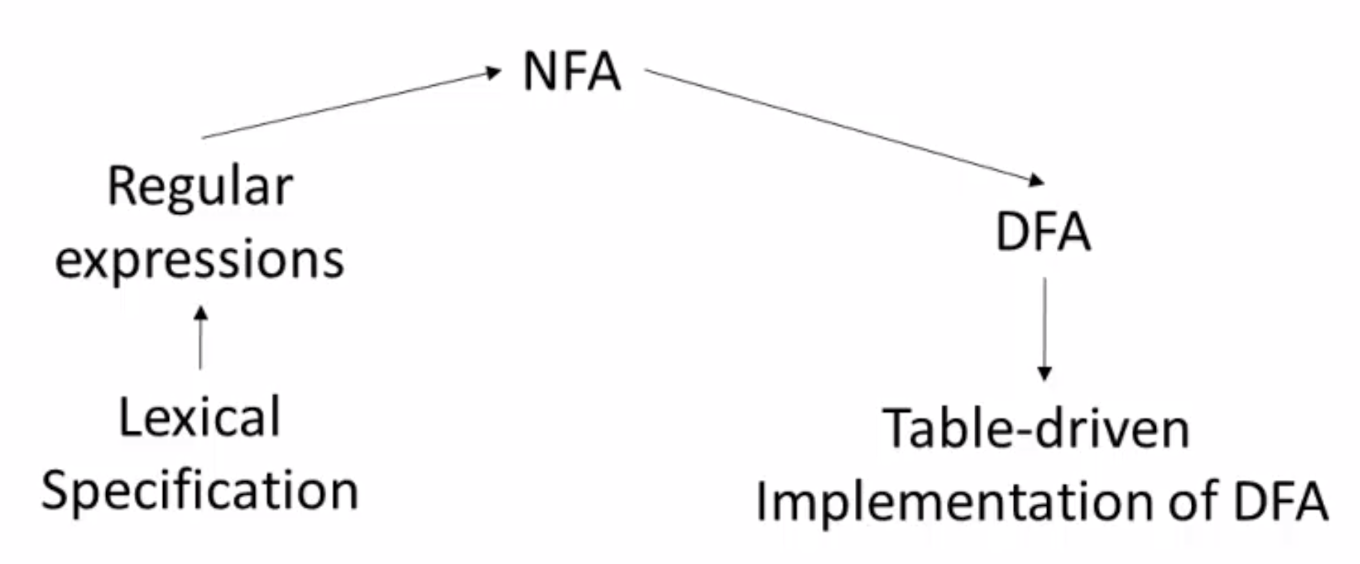
image-20220610115046840
  • 确定lexemes
  • 转换为正规式表达 Regular Languages
  • 转换为NFA
  • 确定化，转换为DFA（实际操作中没有必要，效率过低）
  • 利用二维数组实现 DFA，从而实现一个词法分析器（效率过低），于是考虑二维数组实现NFA即可

输入输出 #

从词法分析到类型转换器的数据流

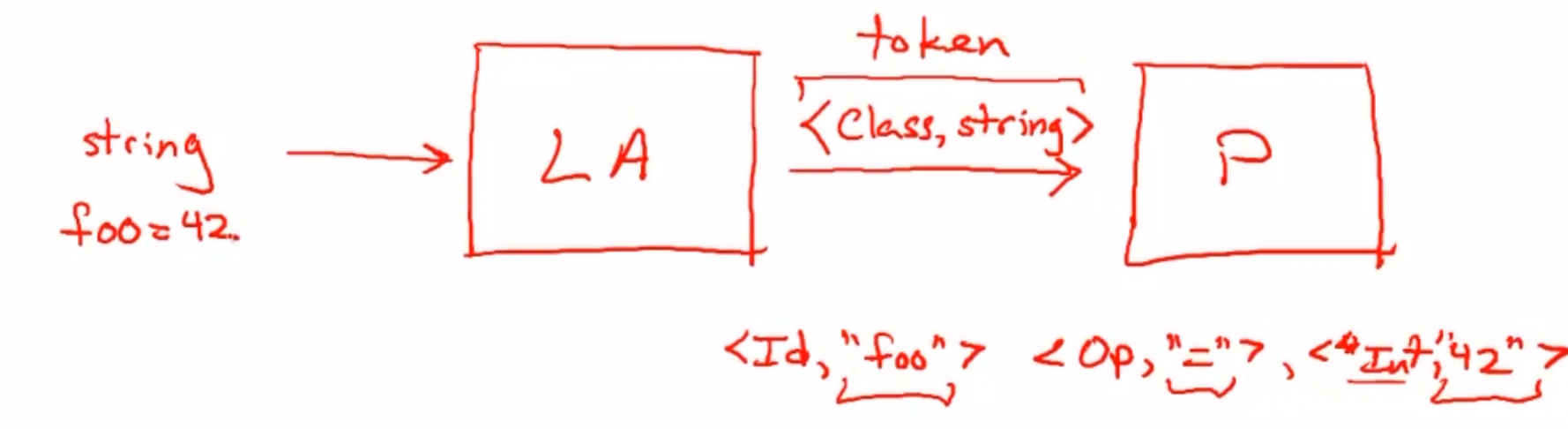
image-20220610093358275

线性string #

输入的内容被看做线性string（即换行、tab都看做是转义字符）。

Token #

对于这些string，LA的任务就是把他们拆解成lexemes组成的序列。

  • token是元组，其由lexeme和其类型枚举构成。

Token中的类型枚举 #

主要是Operator、WhiteSpace、Keywords、Identifiers、Numbers

Regular Languages #

必要性 #

我们需要figure out每个token classe中包含了什么样的lexeme。而且这种规定应当是可以进行匹配的。

构成方法 #

  • 字符
    • ‘c’ = {"c"}
  • 空串
    • ε = {""}
    • 注意，空串不是空集。它是一种特殊字符串。
  • 取并
    • A + B = {a|a in A} or {b|b in B}
  • 连接
    • AB = {ab|a in A and b in B}
  • 迭代（连续出现自身）
    • A^*是A的大于等于1次对自身的连接的并。也就是包含了1次（A^1）、2次(A^2）、…各种连接的结果。
    • A^i是指A对自身的i次连接。

扩展构成方法 #

  • 至少连续出现一次自身
    • A+ = AA*
  • 并的另一种写法
    • A|B = A+B
  • 可选(可能出现，也可能不出现)
    • A? = A+ε
  • 表范围
    • [a-z] = 'a'+'b'+...+'z'
  • 范围的补集
    • [^a-z] = [a-z]的补集

字符集Σ上的语法 #

  • 表示Σ上的语法的最小的正规式集合称为字符集Σ上的语法。

【算法】解析正规式描述的语法 #

  • 首先把给定的各正规式写成其定义式的形式。也就是写成若干集合的形式。
  • 然后，利用正规式的生成规则进行集合运算即可。例如：
image-20220610101111140

Formal Languages #

字符集Σ上的语言 #

字符集Σ上的语言是一系列由字符集Σ构成的字符串构成的集合。

如果说字母表是字符集Σ，那么句子就是字符集Σ上的语言。这些句子由字母表构成的单词短语构成。

字符集Σ例如ASCII，语言例如C++。

正规式的语言（产生式） #

给定描述：L(正规式) -> 对应的set of strings

也就是正规式的语言包括了一系列string构成的集合。（根据语言的定义：是一系列字符串的集合，没毛病）

因此，L就可以看做是一个映射，它把正规式映射到一系列string集合上面。这又称为产生式。

值得注意的是，L是多对一的映射。也就是可以有多个不同的产生式来表达同一种string集合。

  • 字符
    • L(‘c’) = {"c"}
  • 空串
    • L(ε) = {""}
    • 注意，空串不是空集。它是一种特殊字符串。
  • 取并
    • L(A + B) = {a|a in L(A)} or {b|b in L(B)}
  • 连接
    • L(AB) = {ab|a in L(A) and b in L(B)}
  • 迭代（连续出现自身）
    • L(A^*)是A的大于等于1次对自身的连接的并。也就是包含了1次（L(A^1)）、2次(L(A^2)）、…各种连接的结果。
    • L(A^i)=连乘L(A^k),是指A对自身的i次连接。

定义一个语言 #

R = Operator + WhiteSpace + Keywords + Identifiers + Numbers
  = R_1 + R_2 + R_3 + R_4 + R_5

R_1 = '+' + '-' + '*' + '/'
...

可见，用各正规式构成五大元素，然后再并起来即可构成一门编程语言。

【算法】简单词法分析 #

  • 输入：程序string；输出：token
  • 记录起始下标i，不断读入char直到k，检查i到k之间的substring是否属于L(R)。
  • 如果满足，则直接就知道了是属于R_j，j是几，于是就知道这段lexeme是什么元素了，例如是操作符。
  • 利用lexeme和其type生成token，删除输入串中的i到k的substring，返回第一步。

词法分析需要解决的两个问题 #

首先是二义性的消除。

  • 值得注意的是，需要遵从“最长匹配原则”。这是为了防止较短的关键字把较长的关键字给mask了。
  • 此外，还需要遵从“优先级原则”。也就是如果一个lexeme同时匹配了两个R_i，分别是R_1和R_2，例如R_1是Keywords，R_2是Identifiers，那么应当以R_1为准，即其匹配优先级更高。例如在PL0*中，你不能定义一个if作为Identifiers。
  • PL0*是指不能定义和Keywords重复的标识符。但是PL1是可以的。PL的意思是Programming Language。

此外是错误处理与恢复。

  • 例如上述算法中，如果对于L(R)匹配失败，那就得准确地进行报错。

Finate Automata #

FA是来帮助进行词法分析的有力工具。

形式化定义 #

一个有限自动机（FA）由如下部分构成：

  • 输入字符集Σ
  • 有限（Finate）的状态集合S
    • 有限自动机之所以有限，是因为其状态集合是有限集。
  • 一个起始状态n
  • 一些终止状态（Accepting State）构成的集合F
  • 一些状态转移方式构成的集合

状态转移 #

状态转移一般被定义为状态S_1接受了字符输入a，从而转移到状态S_2，记作：

image-20220610110903951

Accepted & Rejected #

如果当前在终止状态上，并且到了读入的末尾，那么称为Accepted。

否则，如果已经到了读入的末尾，却没有在终止状态上，或者没有到读入末尾但是不能转移到其他任何状态（卡住了），则rejected。

图示记法 #

image-20220610111330826 image-20220610111353209

举个例子🌰 #

image-20220610111739006

如图的FA只接受单个1的输入。

  • 如果输入1：那么状态A接受1转换到状态B，Accepted.
  • 如果输入0：那么FA卡住了，寄。
  • 如果输入10：那么FA读入1就转到B了，且B是终止状态，但是当前还没读入到末尾，所以寄

FA的语言 #

因为一个FA只能Accept某一些string构成的集合，想到“集合”就想到了语言！因此，FA也是可以用来定义语言的！

我们称一个FA能接受的string的集合为该FA的语言。

ε-Move（ε边） #

对于ε边，FA可以不接受任何输入而完成该边连接的两个状态之间的转移。

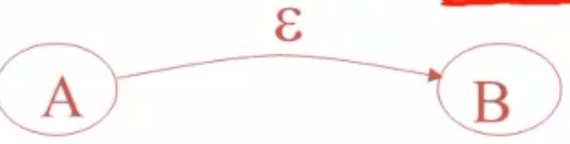
image-20220610112606448
  • 例如，这里A就不需要接受任何输入，即可自己悄没声地转移到B上。

Deterministic Finite Automata（DFA）vs. Nondeterministic Finite Automata（NFA） #

定义 #

DFA是具有下列约束条件的FA：

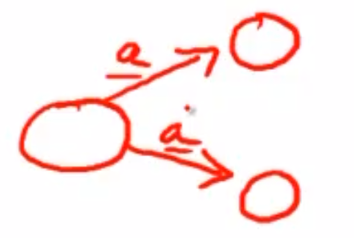
image-20220610112834872

首先，对于当前状态下的一个输入，只可能转换到一种状态。可见，如图的场景是不允许的。

此外，不允许存在ε边。也就是必须要接受输入，才能完成状态转换。

那么NFA的定义就是反之了：即对于给定状态下的一个输入，可以转换到多种状态；并且存在ε边，即可以不接受输入就完成某些状态转换。

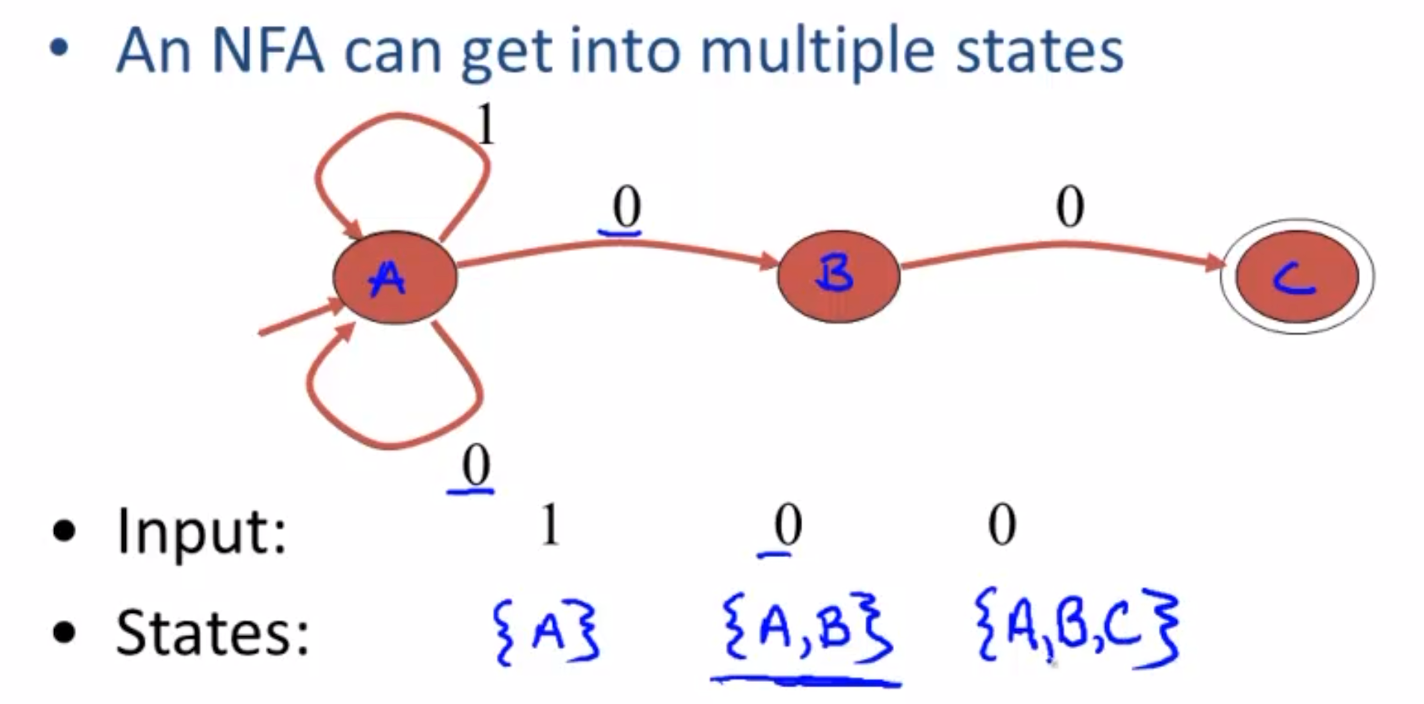
image-20220610114201331

对于如图NFA，其接受1后，可以转换到A，再接受0，则AB，如果接着又接受了一个0，则除了AB还能到C。

DFA和NFA在Accepted上的重要区别 #

对于一个输入，如果可被Accept，它只能对应该DFA的状态转换图中的一条唯一路径。

但是NFA则没有这样的性质。即可能存在多条路径使之被Accept。只要有一条路能在输入末尾时正好转换到终止状态，则称为Accepted。

DFA和NFA的等价 #

  • 他们都能表示同一种语言，只是呈现形式不同。换句话说，存在等价的DFA和NFA。
  • 一般情况下DFA在时间复杂度上更加优秀，因为其转化是固定的，意味着有更快的运行速度。
  • 但是NFA在空间复杂度上更加优秀。等价的NFA可能比DFA指数级别上地小。

从正规式到NFA #

将正规式的运算翻译为NFA的模式 #

image-20220610141018502

首先定义如图的NFA，它的意思是以M为语言的自动机，其中M与某正规式是等价的。这里的箭头是输入，内部的双线椭圆是终态（我们假设只有一个终态）。

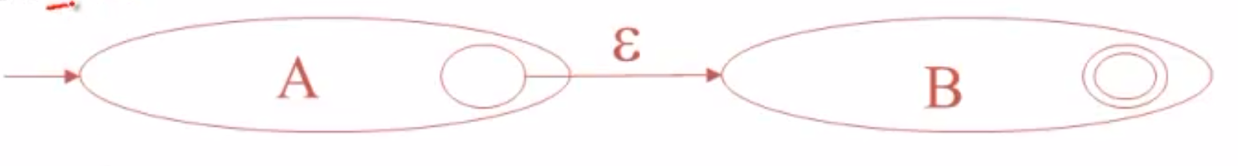
image-20220610141228366

对于AB连接运算，可以如图进行定义。也就是A的终态不再是终态，而是伸出一个ε边链接到B的输入。意思是匹配完了A中的部分，可以无缝切换到B继续匹配而不需要任何额外输入，换言之就是B的部分紧跟A的部分。

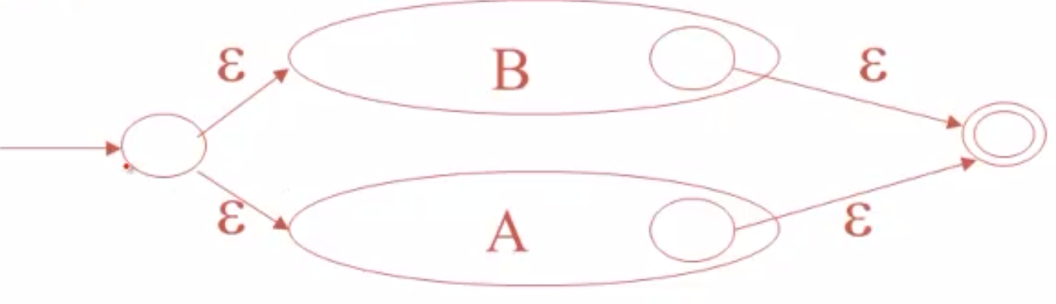
image-20220610141428199

对于A+B运算，引出一个新结点，并用ε边连接他俩，表示可以自由选择A、B表达式进行匹配。当结束后，再用ε边连接到终态。

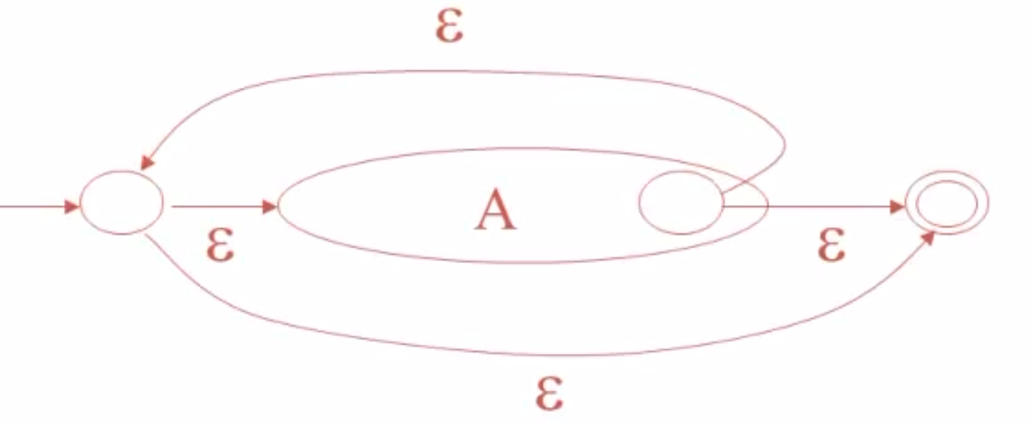
image-20220610141737510

对于A*运算，如图构造。结合其定义进行理解。

从正规式快速构造NFA #

我们已经知道了正规式之间的运算如何转换为NFA模式。那么如果反复套用上述的NFA模式，就可以不动脑子地完成NFA构造。

对于一个复杂的正规式，它可以拆成若干单个的lexeme之间运算的结果。例如(1+0)*1，就可以拆成先1和0做+，然后再自身做迭代，然后再和1做连接。于是可以像这样自底向上地逐步构建NFA的各个部分，最后得到一个完整的NFA。

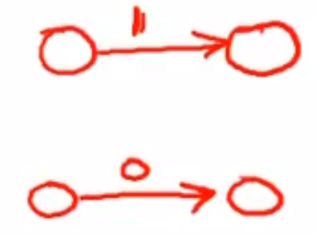
image-20220610142218520

如图，先拿到0和1代表的NFA。这样的NFA专用于匹配单个lexeme，所以一旦输入了要匹配的lexeme，直接进入终态，没毛病。

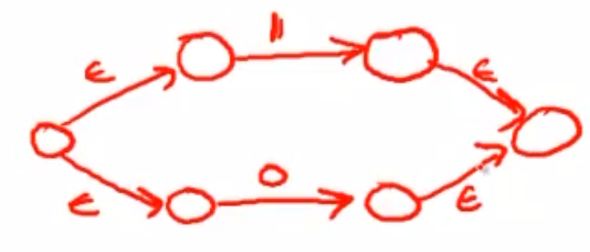
image-20220610142551824

然后，利用上面的“+”规则，将代表0、1的两个NFA套上“+”模式。

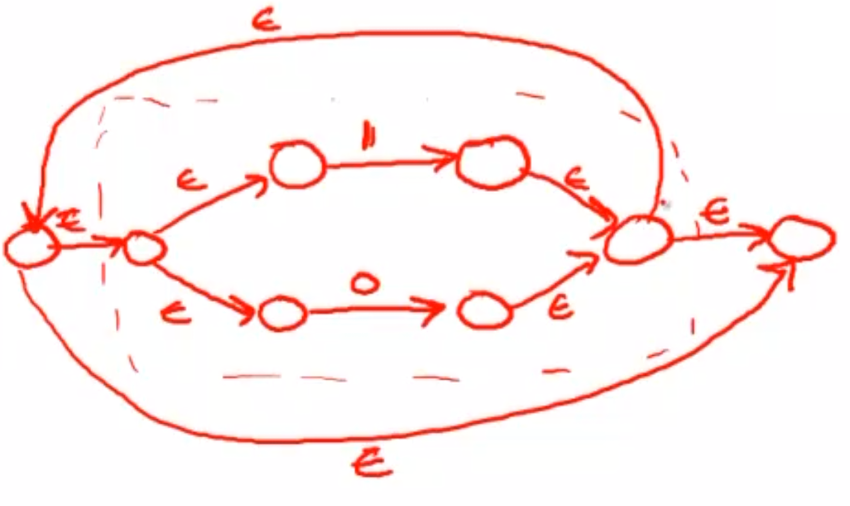
image-20220610143249116

然后，利用上面的“迭代”规则，将上一步的复合NFA再套一层“迭代”模式。

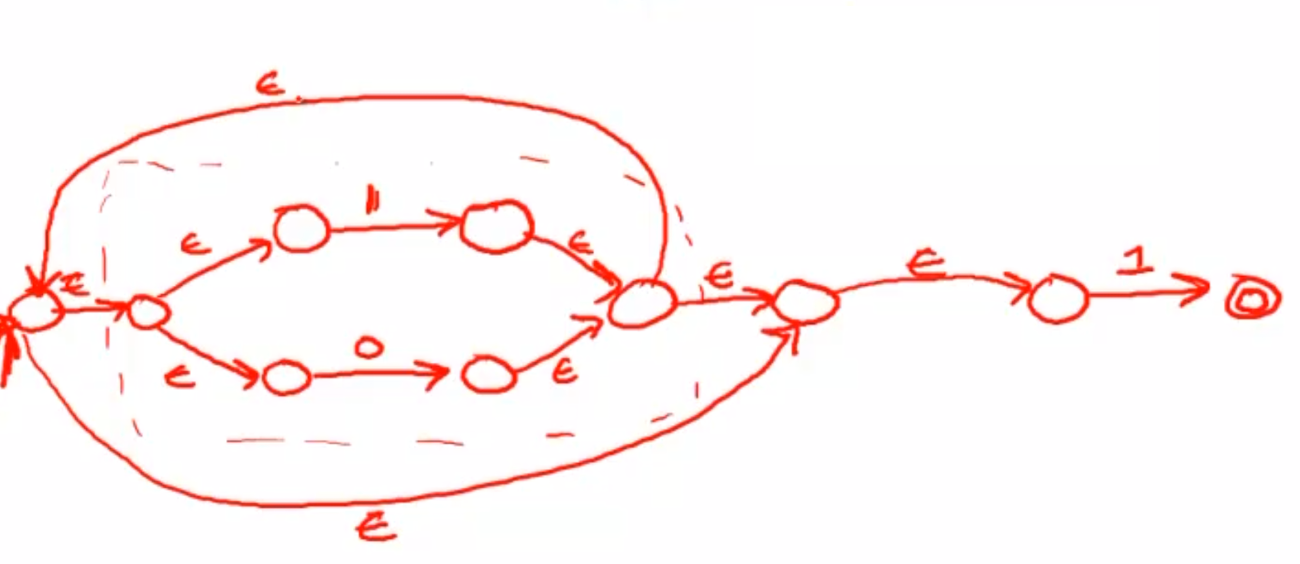
image-20220610143416253

同理，再构建一个匹配“1”这个lexeme的自动机，再套“连接”模式，补充终态和初态，整个NFA就构造完成。

从NFA到DFA #

ε-闭包 #

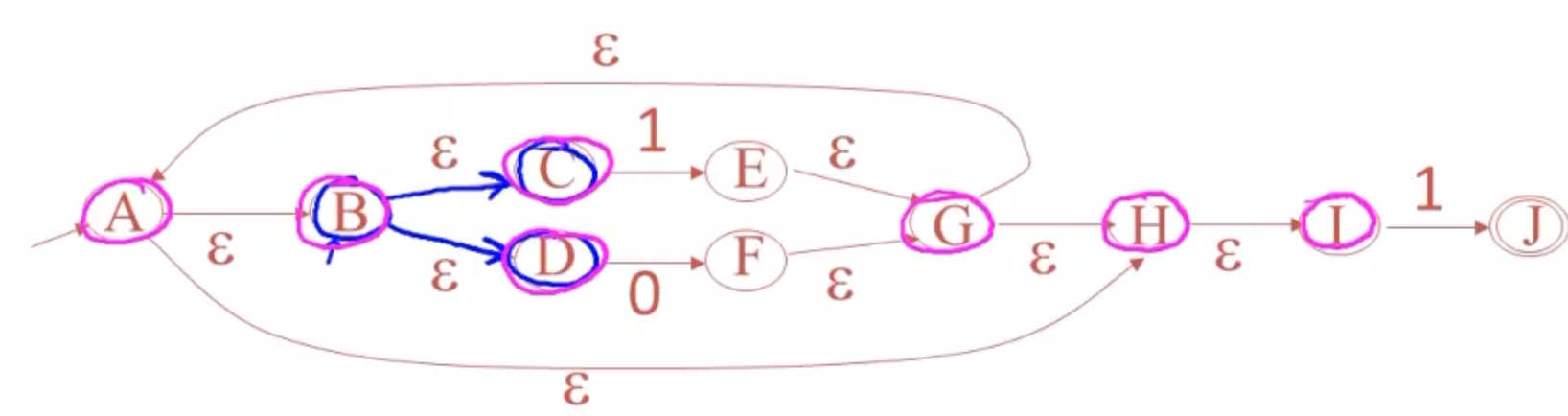
image-20220610143834972

点P的ε-闭包是指包括P本身的通过ε边可以到达的所有状态。注意，这个过程是递归的，可能一步就找全，也可能递归很多步才能找全。

  • 例如B的ε-闭包只包含C和D，因为其他点就无法通过ε边到达了。
  • 而G的ε-闭包首先包含了H和A，H又到I，A又到B，B又到CD，所以图中粉色的都是G的ε-闭包。

寻找ε-闭包的技巧在于盯紧每个相关点的出度。只要不落下任何一个出度，就没有问题。

NFA在同一时刻可以同时处在一个ε-闭包中的状态中 #

在某一时刻，NFA可以认为是同时处于某ε-闭包中的所有状态。

换言之，NFA可以同时处于其状态集合S的幂集中的任意集合包含的状态中。

对于n个状态的NFA，其状态集合有2^n-1个子集，所以其可能处于的状态有2^n-1种可能。

换种方式理解：对于n个状态的NFA，每个状态都有被处于和不被处于两种情况，所以共有2^n种可能。去除“任何状态都不被处于”的这种不可能情况，即有2^n-1种可能。

从ε-闭包下手转化到DFA #

既然NFA在同一时刻可以处在很多状态中，即一个ε-闭包中，那么如果能把ε-闭包构成状态，重新做一个FA出来，那不就转化到DFA了吗。

因此，可以预见，对于FA的构成元素，会有如下的转变：

  • NFA的各个状态分别是S的元素，但是DFA的状态变成了S的子集（即其ε-闭包），而不仅是元素了。
    • 特别地，初始状态s变成了s的ε-闭包。
    • 一般地，任意状态t变成了t的ε-闭包。
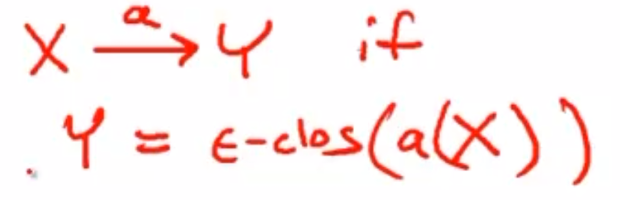
image-20220610150723221
  • 状态转换关系变成如图所示的样子。也就是X通过输入a转换到了某个状态，如果Y也属于在NFA中的这个状态的ε-闭包，那么这个状态转换是成立的。
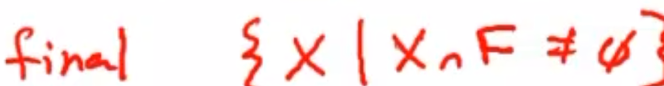
image-20220610150915927
  • 最终状态如图定义。

举个例子🌰 #

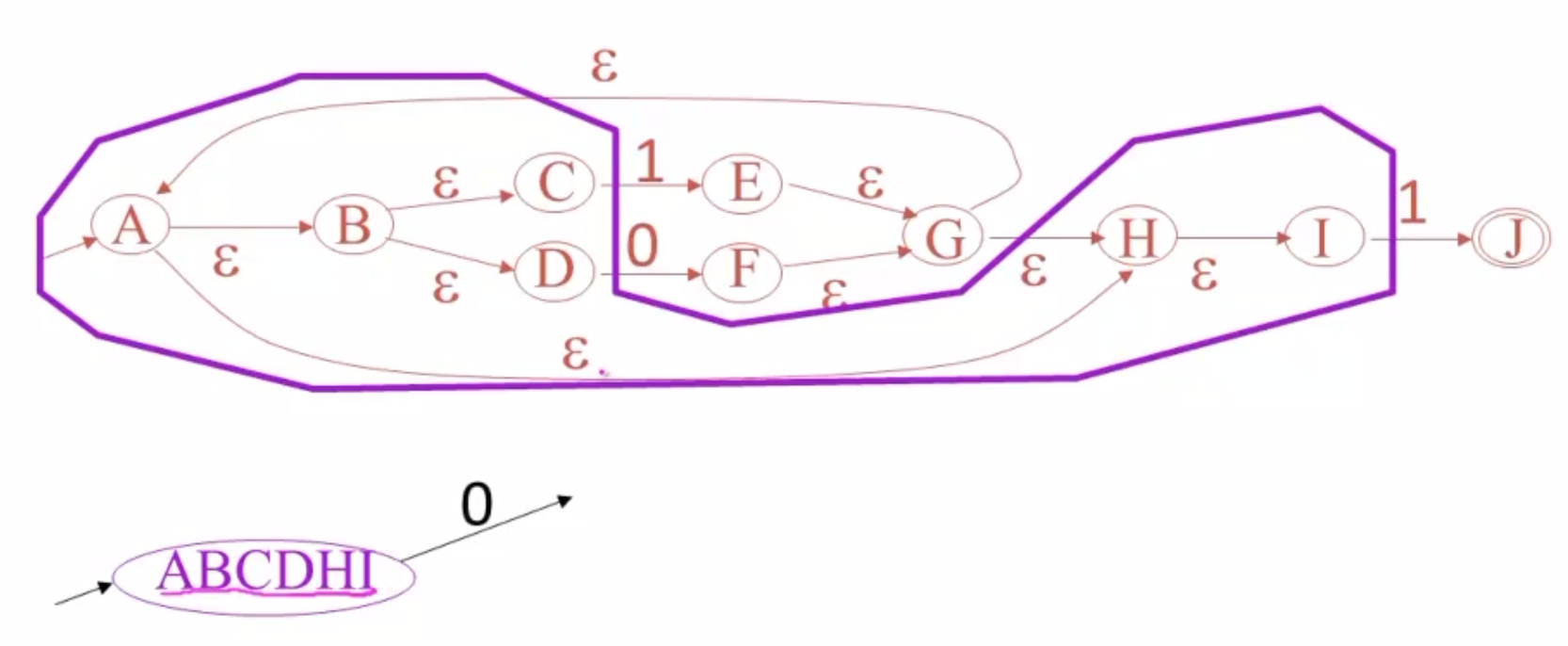
image-20220610151459351

我们先寻找起点的ε-闭包，这样可以用来构造DFA的起点。

如图，紫色部分是A的ε-闭包，包括ABCDHI。

现在，观察该闭包发出的边，可以看到其能够接受1或0.

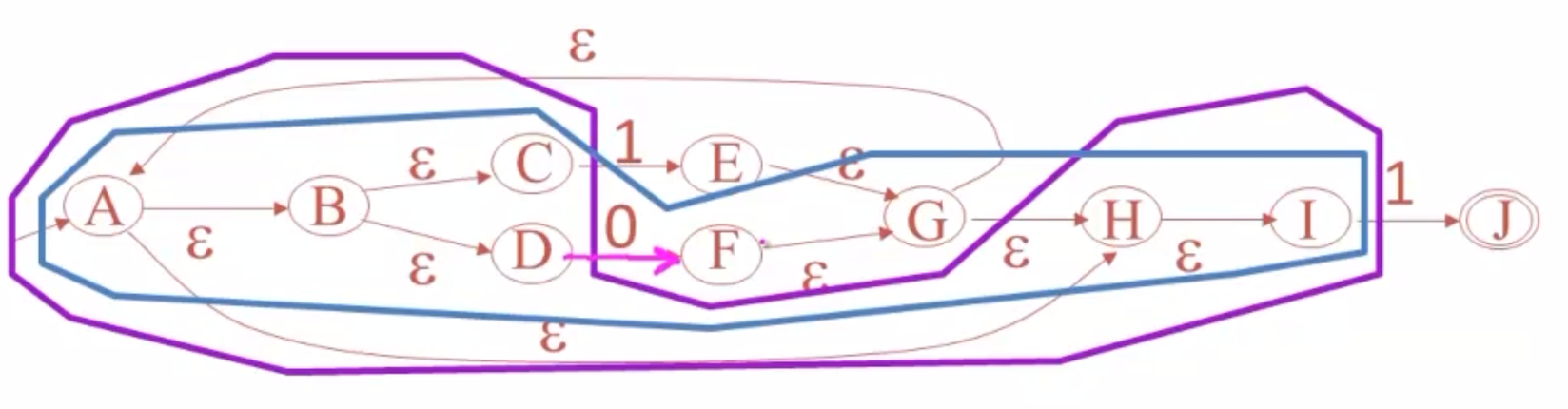
image-20220610151751672

首先考虑接受0的情况，它会转到状态F，而F的闭包如上图，包含了FGHIABCD。把这个新闭包作为一个新的状态，放入DFA：

image-20220610151932380

再考虑接受1的情况，它会转到状态E，E的闭包是DGHIJABCD，创建新的DFA结点。

值得注意的是，因为E闭包内包含了终态J，所以被认为是DFA的一个终态，所以在DFA中为双线椭圆。

image-20220610152036227

继续观察非ε边。

  • F闭包有非ε边0（从D出，进入F闭包）和1（从C、I出，进入E闭包）；
  • E闭包有非ε边0（从D处，进入F闭包）和1（从C、I出，进入E闭包）；

值得注意的是，上述两条观察结果非常相似。这是因为ε-闭包可能很大，所以就算需要观察很多边，但是往往都不需要重复寻找新闭包。

值得注意的是，需要寻找的不是从闭包内指向闭包外的边，而是以闭包内的状态为起点的任意非ε边，不论是指向了闭包内的状态还是闭包外的状态。

  • 如果是指向闭包内状态的，就在DFA相应位置体现为自环；
  • 如果是指向闭包外状态的，就在DFA的不同状态之间建立边。

依照上述理论，把这些关系建立新边，分别体现在DFA中，DFA就构建完成：

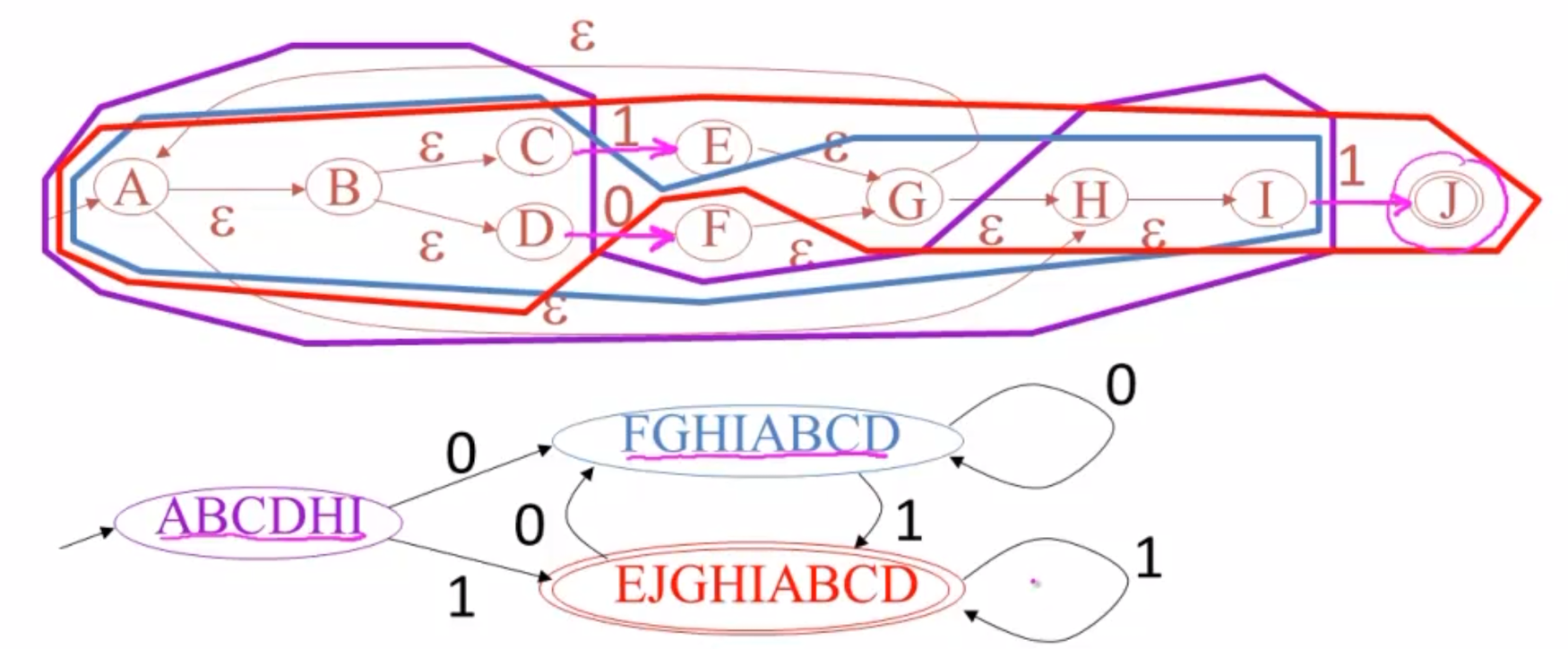
image-20220610152110053

DFA如何与NFA进行等价 #

  • 观察上述例子可以看出，DFA把每个用到的ε-闭包作为状态（注意不可能是全部ε-闭包，因为它有 2^n-1种）。因为NFA同一时刻只能处于同一ε-闭包中，这就决定了该DFA在每个时刻只能同时处于一个状态，这就达到了目的。
  • 换句话说，DFA通过提取ε-闭包作为状态，模拟了一个NFA出来。

利用二维数组实现 NFA #

建立表格来记录状态转移 #

image-20220610153416897

对于一个DFA，在状态i下，输入a，如果能转移到状态k，那么就可以如图进行记录。

这个表格的不同行是不同的states，不同列是不同的输入。元素记录了转移目标状态。

是否有必要转换成DFA来实现一个词法分析器？ #

实际上不一定需要这么做。因为NFA可以同时处在的状态有 2^n-1种不同的情况，也就是可能存在 2^n-1种ε-闭包。

这会导致指数爆炸式的内存消耗，因为最坏情况下，存储一个n状态的NFA等价的DFA是2的指数的空间复杂度，这难以接受。

所以，可以考虑从NFA开始，直接实现词法分析，而直接跳过DFA。

利用二维数组实现NFA #

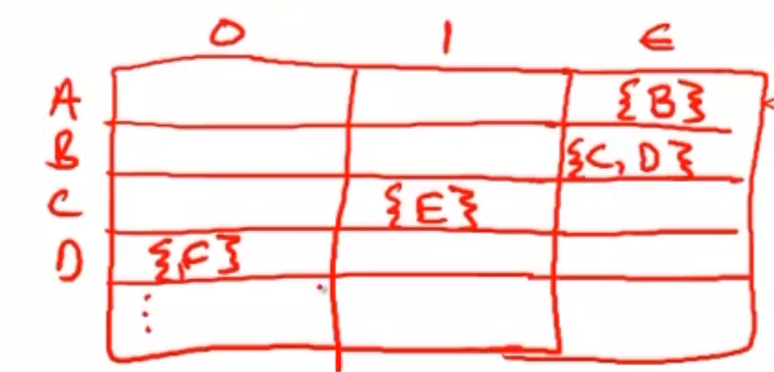
image-20220610154639637
  • 因此，只需要建立如图的表格，来实现一个NFA。值得注意的是，它不会存在指数级别的空间复杂度，因为它的大小只是状态数和lexeme数的乘积而已。
↑