↓Skip to main content
A cup of beer
  1. Posts/

做个编译器——自底向上语法分析

·258 words·2 mins
笔记
Table of Contents

注意：本文中，“栈顶子串”和“栈顶符号串”是一个意思。

General #

自底向上分析是当前大多数编译器在使用的语法分析方法。

我们的工作重点在于寻找句柄。因为它能指导我们何时进行归约操作。

它可以正确处理带有左公共因子的情况，同时具有上一章节中LL0的优点：一遍扫描，look-ahead。

image-20220612092815029

如图是自底向上分析的一个例子。之前我们介绍的方法是自顶向下的，区别在于这里是从输入串入手，逐步归约到开始符号。

如果反过来看这个过程，这是一个最右推导。因此这是一个反向最右推导（最左归约）。

移进-归约方法 #

归约和推导 #

Reduction and Derivation

推导是从非终结符开始的，归约是从终结符或非终结符或其组合开始的。（根据产生式两边可容纳的符号类型给出。）

最左归约的一个性质 #

对于形如αβω的情况，如果下一次归约使用了产生式X-> β，那么ω 必然是终结符（串）。

这是因为它遵循反向最右推导。如果ω不是终结符，那么应该对ω进行归约，而不是 β。

将输入串分割成两个子串 #

假设输入串是被原地修改的。那么存在一个下标，使得它的左边是已经被处理过的，是非终结符和终结符构成的子串；它的右边是暂时还没进行处理的，是由原始输入串构成的，显然都是终结符。

这体现了最左归约的定义：我们是对于输入串从左到右地寻找可进行归约的终结符来进行归约的。

因此，这个位置就是下一个需要进行归约的符号的位置。其左边因为遵循最左归约，都尝试过了；其右边还没被扫描到。

移进和归约 #

Shift and Reduce

移进

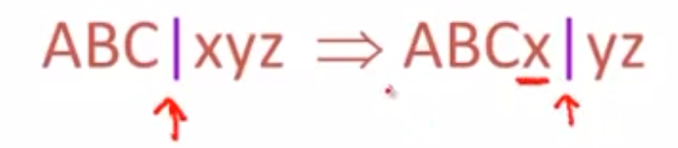
image-20220612094836611
  • 向右移动一步分界线。也就是有一个新的未处理的符号进入到了左边。

归约

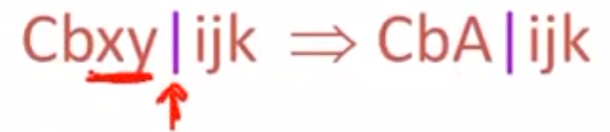
image-20220612094940839
  • 对于从分隔符开始，向左一段的连续子串而言，如果有匹配的产生式，则进行归约（把他们就地替换成产生式的左部）。
  • 再次强调，被归约的连续子串的右边下标必然是分隔符。

代码实现 #

因为只需要对以分隔符为结尾的子串进行归约，而不需要对更靠左边的其他部分进行操作，所以可以用一个栈来实现分隔符左边的部分。

因此，移进就是push进一个新的，而归约就是先pop右部，再push左部。

两个冲突 #

如果在当前情况下（对应分析表单元格），无论是移进还是归约都是可行的，这称为移进-归约冲突。这种冲突可以被消除（引入优先级声明），而且如果出现，属于正常现象。

如果在当前情况下（对应分析表单元格），可以由两种产生式来进行归约，称为归约-归约冲突。这种冲突无法消除，说明文法上面有严重的问题，需要从文法上面彻底修改。

只要出现上述冲突，就说明在同一状态下有多重转移方式，此时编译器就不知道如何采取措施了。

句柄 #

自底向上分析是有条件的最左归约 #

它并不是从左向右找终结符，看到一个终结符就立马归约他。而是根据一张分析表，来看是不是在当前情况下有必要归约他。如果不需要，那就跳过他继续向右扫描。这个所谓继续向右扫描就是“移进”。

image-20220612100850901

例如如图文法。如果现有int#*int+int，其中#是分割线（栈顶）。如果现在直接进行归约，则使用产生式T->int，变成了T#*int+int。然后就会发现，基于给出的产生式，之后无论怎么做，都不可能归约到开始符号E上面了。

这就意味着并不是看到能套上的产生式就立即对栈顶子串进行归约，因为盲目的归约会导致走进死胡同。

何时可以进行归约 #

如果有S-*>αXω ，而αXω->αβω ，那么当栈顶情况是形如αβ#ω （其中#是栈顶分隔符，α是任意长度的符号串，ω 是任意长度的终结符串）时，进行归约是没有问题的，因为存在从开始符号S到αX的星号推导，意味着归约以后，是可以推回到开始符号S上的。换言之这个归约是安全的。

其中，αβ称为αβω 的一个句柄（handle）。实际上，从形象的角度上说，翻译成“把手”可能更加合适，因为这意味着出现αβ#ω（其中#是栈顶分隔符）的时候，可以以αβ为抓手进行归约。

句柄的定义📔 #

句柄是可进行安全归约的栈顶子串。

句柄是指能够允许将来的归约能够回到开始符号上的归约对象（产生式的右部），如果栈顶子串是一个句柄，那么才可以归约，否则会进入死胡同。

移进-归约关于句柄的性质 #

  • 句柄必然是栈顶子串，不可能出现在栈的其他部位。否则一路走来，早就把它归约了，还用等现在？
  • 每次归约后，栈顶子串就被替换成了非终结符，然后需要进行新的移进操作来在栈顶积累出新的子串，当这个子串是句柄的时候就可以进行下一步归约了。循环往复，直到归约到开始符号，就可以完成语法分析。

寻找句柄 #

目前没有通用的算法来快速找到句柄。但是对于上下文无关文法，当前有一些靠谱的方式来猜测哪些是句柄，并且准确率可以达到100%。

产生式右部前缀 prefix #

任意时刻，栈顶的位置可以抽象成α|ω ，而α称为一个可行的前缀，意思他是某产生式的右部的前缀，只是还缺少几个符号来组成这个右部，而一旦组成就可以被归约了。

因为任意长度的栈顶符号串都有被归约的可能，而且他们目前还没有凑成一个完整的右部，所以还没有被归约。因此可以引入一种结构来动态跟踪各栈顶符号串的匹配情况，如果完全匹配了就可以归约了。

LR(0)项目 #

LR(0) items.

例如对于X->αβγ，它有几种状态的前缀，分别是：

X->.αβγ
X->α.βγ
X->αβ.γ
X->αβγ.
  • 以X->α.βγ为例，它的意思是目前，以α的长度为长度的栈顶符号串是α，目前正在期望βγ的到来，从而凑出完整右部。
  • 对于X->αβγ.状态，就是可以进行归约的了。
  • 对于X->.αβγ状态，可以认为匹配它的栈顶符号串目前长度是0，或者说匹配他的栈顶符号串是ε。

特别地，对于X->ε，只有一种前缀即X->.。这意味着可以立即开始归约。

这些前缀称为LR(0)项目。

前缀增长 #

凑出右部有，但是前缀还暂时没有的符号的过程，**称为前缀增长。**每次前缀增长，就是那个“点”向右移动的过程了。以下是实现前缀增长的两种方式：

  • 一种是做移进从而让α增长；
  • 另一种就是如果α内部有某前缀凑成了一个句柄，归约之，于是这段栈顶子串被替换成一个新的非终结符。
  • 第一种方式补充了终结符，第二种方式把一段栈顶子串替换成了非终结符（根据产生式的定义，产生式左部只能是非终结符）。

前缀和句柄的关系 #

产生式右部前缀不一定是句柄前缀，因为并不能保证在当前状态下利用该产生式进行归约就一定能回到开始符号上。

只有在这些产生式右部前缀中，只有句柄前缀能够最终拼凑出完整的右部来，从而完成归约，其他的都可能半途而废，从而防止采用他们的归约。这样才能保证不会进入死胡同。

实际上，可以这么定义：能增长出完整右部的前缀才是句柄；增长不出完整右部的前缀必然不是句柄。

前缀层级关系：如何通过前缀增长来实现到达开始符号的整个归约过程 #

根前缀就是开始符号S的产生式右部的前缀。句柄前缀都应该看做根前缀的孩子，因为应当通过句柄归约到开始符号上来，而不是任意的产生式右部。

刚才提到了，如果栈顶子串内部有某前缀凑成了一个句柄，归约之，于是这段栈顶子串被替换成一个新的非终结符。这导致其祖先前缀也可能发生增长。如果一个祖先的前缀增长，使之凑出了完整右部，进行归约，就可能因为栈顶子串的变动进一步导致它的祖先的前缀增长，从而又引发….，以此类推。如果无法这样推下去，就可以移进，寻找新的机会。最终，让根前缀增长到它的完整右部，就完成了整个输入串的归约过程了。

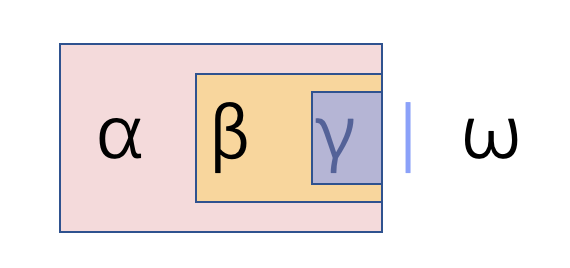
image-20220612111457973

举个例子🌰，如图，粉色、黄色、蓝色这三个子串都是栈顶子串，因为他们的右端点都是栈顶，只是长度不同而已。作为栈顶子串，他们都是有可能被归约的对象，因此都被认为是右部前缀。

  • 粉色栈顶子串是αβγ，黄色栈顶子串是βγ，蓝色栈顶子串是γ。
  • ω是暂未处理的输入串部分（栈外部分）。

现在，如果γ已经成功增长到了右部，则可进行归约，如果有产生式X->γ，那么γ被替换为X，那么黄色栈顶子串变成了 βX，粉色栈顶子串变成了 αβX，

此时，如果 βX又恰巧是一个右部，例如有产生式Y-> βX，那么黄色也被归约了，替换成Y，那么粉色栈顶子串变成了αY。

以此类推。最终如果连开始符号的右部也被凑出来了，那语法分析就顺利结束了。

LR(0)分析法 #

所有的前缀都是上下文无关文法表示的，属于正规式的形式，可以被FA识别。因此我们考虑用FA来进行SLR分析。

拓广文法 #

为了统一化表示各状态，给开始符号S之前再加一个S’状态，且有S'->S，这样一来开始符号S也可以被归约了。这样一来，任何符号都能被归约了。

有效的LR(0)项目 #

所谓有效，是指该LR(0)项目对特定的前缀有效。如果不落实到具体前缀上，有效性是无从谈起的。因为所谓有效，就是该前缀能匹配该LR(0)项目，且如果增长完成，用它能够最终归约到开始符号上。

对于前缀αβ，如果有S'-*>αXω,X->βγ ，其中X是非终结符，ω是终结符，则项目X->β.γ对于前缀αβ而言是有效的，因为可以归约到开始符号上面。

在SLR自动机中，An item I is valid for a viable prefix α if the DFA recognizing viable prefixes terminates on input α in a state s containing I.（DFA在读入α后进入了状态s，而这个状态s包含了项目I，那么项目I对于α而言就是有效的。）

The items in s describe what the top of the item stack might be after reading input α.（DFA的状态中包含的项目可以预示在该状态下读入α后，栈顶符号串会变成什么样子。）

值得注意的是，一个LR(0)项目可以对很多前缀而言都是有效的。例如项目T->(.E)对于1个、2个、…、n个连续左括号构成的前缀都是有效的，因为他们都表示”刚才接收了一个左括号，现在在期望接收其他的符号“。

构造LR(0) NFA的思想 #

构造一个NFA来指导归约。这个NFA的state是各LR0项目。特别地，其开始状态是S'->S。我们需要建立他们之间的转化关系，例如对于LR0项目E->α.Xβ构成的state：

  • 【建X边：设置上一轮移进或归约结束后，文法符号栈栈顶就是X的情况下的状态转移】建立一条X边，指向E->αX.β这个state，意思是在当前状态下如果遇到X，转移到下一个状态。
  • 【建ε边：设置上一轮移进或归约结束后，文法符号栈栈顶不是X的情况下的状态转移】如果X是非终结符，那么X会有若干产生式。则应当建立从当前状态E->α.Xβ指向每个这样的产生式，例如X-> γ的首个项目构成的状态，即X-> .γ的ε边。

建ε边的原理是：因为X是非终结符，就算栈顶不是X，也可以抢救一波！

  • 也就是说，可以假设栈顶那段不是X的子串是由X推导出来的。因此可以自身加ε边，不带任何成本地自动转到对X的各产生式的归约上来。
  • 按照这条路，只要归约成功了X的产生式，得到了X，就可以退回到刚才那个状态了，而且现在这不是有X了吗，所以可以直接走建立的X边，继续下面的归约过程了。

换言之，从状态A建ε边指向状态B的作用在于分而治之。相当于B是A的子前缀，先把精力放到对B的归约上来。只要B归约出来了，A就可以继续进行归约了。这里的思想可以参照”寻找句柄——前缀层级关系“里面说的。

LR(0) DFA #

对SLR NFA进行ε-闭包合并，即可得到SLR DFA。

值得注意的是，SLR DFA的state是若干LR0 item构成的集合。

移进项和归约项 #

形如X->β.的LR0项目，即增长完成的项目，即可直接进行归约。DFA遇到这种项目就执行归约。

形如X->β.tω 的LR0项目，即点的后面是终结符的项目，DFA遇到了就直接移进即可。因为后面是终结符。

LR(0) DFA分析的冲突情况 #

归约-归约冲突

  • 如果某个状态同时拥有多个归约项，那就是冲突了

移进-归约冲突

  • 如果某个状态同时拥有归约项和移进项，那就是冲突了

代码实现 #

goto table

  • 事实上，DFA的各转移边都被存储在goto表里面。即goto[i,A] = j的意思是从状态i到状态j有A边。

action table

  • action[i,A]记录了在状态i下，在接受输入A的时候，应该做什么操作。这种操作可以是移进某符号或归约某产生式。

SLR分析法 #

Simple LR

SLR分析法是对LR(0)分析的改进，其消除了一部分的移进-归约冲突。

相较LR(0)的改进 #

修改了归约的准则。假设当前要处理的输入符号是t，那么对于形如X->β.的状态，不能见到就归约了，而是还要保证t在follow(X)中。

因为保证了这一点，所以能从S星号推导出形如γXtω的情况，其中 γ、ω 任意。于是，下一符号是t，就可以直接跟着X一起归约了。

否则，如果不是这样，你把β归约成X是没有意义的，因为不会为下一步的其他归约创造遍历。

这样一来，就减少了很多归约状态，于是就降低了移进-归约撞车的概率。

SLR文法 #

如果这样降低了概率了，还会出现移进-移进冲突或移进-归约冲突，那么当前文法肯定不是SLR CFG（简称SLR）文法。

但是注意，大多数语言都不是SLR的，包括所有二义性的语言都不是SLR的。

引入优先级声明以适配SLR💁‍♂️ #

如果要对任意的语言解决冲突，使之变成SLR的，可以通过增加符号优先级声明等方式实现。

例如加法、乘法、括号文法就是一个二义性文法，因此它本身不是SLR的：

E -> E+E | E*E | (E) | int

于是在SLR DFA的某state下会同时存在如下LR0项目：

E -> E*E.
E -> E.+E

存在移进-归约冲突。但是如果规定乘法的优先级大于加法，我们就可以去做归约，而不是移进。于是解决了冲突，从而适配了SLR。

↑